Orthocenters and Circumcircles

By:

Brandt Hacker

For this assignment we will examine what happens when we complete the following:

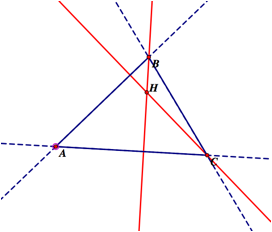
1. Construct any triangle ABC.

2. Construct the Orthocenter H of triangle ABC.

3. Construct the Orthocenter of triangle HBC.

4. Construct the Orthocenter of triangle HAB.

5. Construct the Orthocenter of triangle HAC.

6. Construct the Circumcircles of triangles ABC, HBC, HAB, and HAC.

7. Conjectures? Proofs?

For further reading on altitudes and how to construct them, click HERE(link assignment 4). We start by creating triangle ABC. After creating triangle ABC, we create the orthocenter H.

After creating the altitude, point H, we now have three new triangles that are created involving the orthocenter as a vertex. Below is an image of the three new triangles as well as an image with the orthocenter of triangle AHC.

In the second image shown above we see that the orthocenter of the yellow triangle, AHC, is in fact point B, the third vertex of the original triangle. The same holds true for triangles AHB and BHC, the unused vertex of the original triangle becomes the orthocenter of the new triangle.

Next we will look at what happens if we create circumcircles around each of the four triangles pictured above. When we create the circumcircles for the original triangle (ABC) and the three triangles that involve the orthocenter, point H, we get the following construction:

After constructing these circumcircles we will next look at what happens when we connect the centers of the circles with the vertices of the triangle.

After connecting the centers of the circumcircles to the vertices of the triangle we are left with a hexagon. While it may seem obvious that connecting 6 points will give us a six-sided figure, what is interesting is that this particular hexagon is equilateral. While it is equilateral, it is not a regular hexagon because of the fact that all of the interior angles of the hexagon are not equal to one another.

What kind of triangle would yield a regular hexagon? After playing around with the GSP file, as you can do HERE (link A8threetriangles), we see that the vertices and circumcircle centers of an equilateral triangle produces a regular hexagon. This has been captured in the image below.

Now, what if instead of wanting to create a regular hexagon from the image, we instead want to create a parallelogram? What type of triangle would lead to such a construction? In order for the hexagon to become a parallelogram we would want one of the vertices to be collinear with the center of two of the circumcircles. We would also want the center of the remaining circle to be collinear with the remaining two vertices of the triangle. The only way to accomplish both of these tasks would be to make triangle ABC a right triangle. Notice that for any right triangle the orthocenter H will be the same point as the third vertex, in this case B and H are the same point.

An equilateral triangle allowed us to create a regular hexagon. A right triangle allowed us to make a parallelogram. See if you can determine what specific type of triangle ABC would have to be to allow us to make a rectangle?

Return to Hacker